9-0. あらすじ
9-1. t検定(対応なし)
2つのデータの平均に差があるかを調べる方法。t検定の使い方を学ぶ。
9-2. 分散分析(1要因)
2つ以上のデータの平均に差があるかを調べる方法。分散分析の使い方を学ぶ。
9-1.t検定
t検定とは、2つのデータの平均に差があるかないかを調べる方法である。
2つのデータから『t』を計算する。そしてt分布での『t』の位置を調べることで、平均における差の有無が分かる。
『t』の計算方法
一度に計算すると大変なので、何段階かに分けて計算する。
まずは・・・
① データの個数を求める。(=COUNT) またデータの個数から1を引いた数値も計算する。
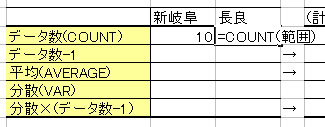
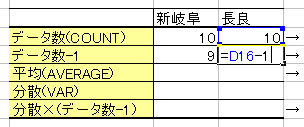
② 平均(=AVERAGE)と分散(=VAR)を計算する。
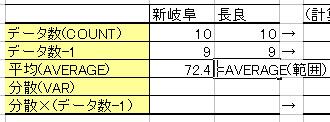
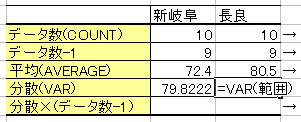
③ 分散×(データ個数-1)を計算する。
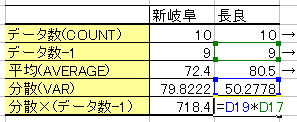
次に・・・
④ ①で計算した2つのデータの個数の逆数を計算して足す。
(データの個数が16と13の場合は、(1/16)+(1/13)と計算する)

⑤ ①で計算した各データの(個数-1)の和を求める。
(データの個数が16と13の場合は、(16-1)+(13-1)=27と計算する)

⑥ ②で計算した2つの平均の差をとる。

⑦ ③で計算した2つの数値を足す。
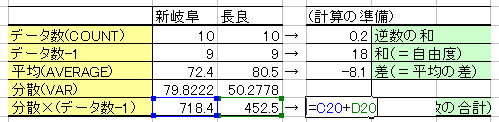
最後に・・・
⑧ ⑦を⑤で割る。
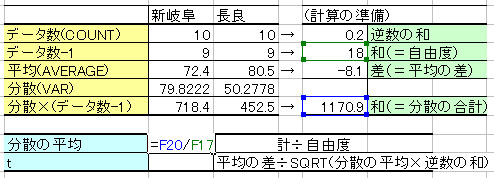
⑨ ⑥を(⑧×④の平方根)で割る。

⑩ tが求まる。
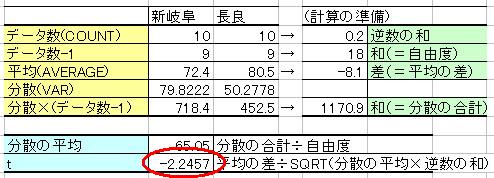
実際は何もない状態からtを計算するのは難しい。そこで・・・
以前にt検定を行ったファイルなどを見ながら、新たなt検定を行う!
t分布の見方
少し甘め(有意水準5%)で調べる場合と、厳しめ(有意水準1%)で調べる場合の2つが選べる。
計算して求めた『t』の値が、
t分布のグラフの○部分(棄却域)に来るかどうかで、2つの平均に差があるかが分かる。
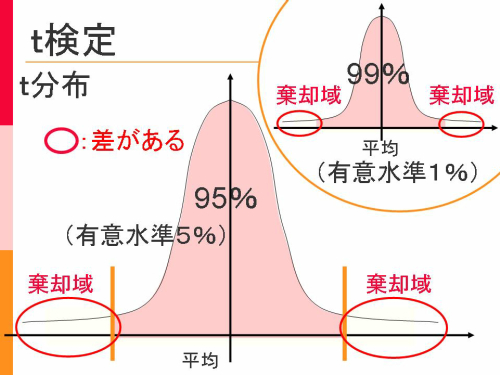
○部分(棄却域)の境界点は、t分布表から求まる。
Excelで『t』を求める際に、求めた『自由度』から境界点が分かる。
t分布表 |
||
| 自由度
|
有意水準5%
|
有意水準1%
|
1 |
12.706 |
63.657 |
2 |
4.303 |
9.925 |
3 |
3.182 |
5.841 |
4 |
2.776 |
4.604 |
5 |
2.571 |
4.032 |
6 |
2.447 |
3.707 |
7 |
2.365 |
3.499 |
8 |
2.306 |
3.355 |
9 |
2.262 |
3.250 |
10 |
2.226 |
3.169 |
| 11 |
2.201 |
3.106 |
| 12 |
2.179 |
3.055 |
| 13 |
2.160 |
3.021 |
| 14 |
2.145 |
2.977 |
| 15 |
2.131 |
2.947 |
| 16 |
2.120 |
2.921 |
| 17 |
2.110 |
2.898 |
| 18 |
2.101 |
2.878 |
| 19 |
2.093 |
2.861 |
| 20 |
2.086 |
2.845 |
21 |
2.080 |
2.831 |
22 |
2.074 |
2.819 |
23 |
2.069 |
2.807 |
24 |
2.064 |
2.797 |
25 |
2.060 |
2.787 |
26 |
2.056 |
2.779 |
27 |
2.052 |
2.771 |
28 |
2.048 |
2.763 |
29 |
2.045 |
2.756 |
| 30 |
2.042 |
2.750 |
| 40 |
2.021 |
2.704 |
| 60 |
2.000 |
2.660 |
| 120 |
1.980 |
2.617 |
| ∞ |
1.960 |
2.576 |
境界点は =TINV(0.05, 自由度) もしくは =TINV(0.01, 自由度) としてExcelで求めることもできる
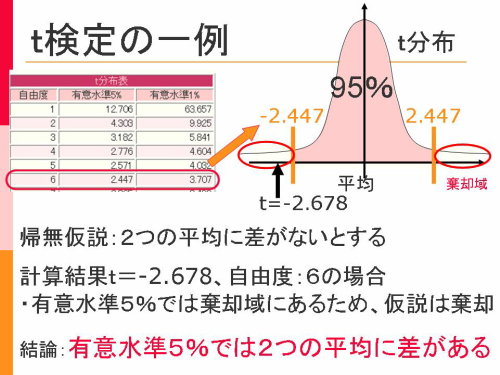
結論は3パターン
・有意水準5%で棄却域に入らない
→2つのデータの平均に差はない。
(有意水準5%で棄却域に入らないならば、有意水準1%でも棄却域に入らないため、5%だけでよい)
・有意水準5%で棄却域に入るが、有意水準1%で棄却域に入らない
→有意水準5%では2つのデータの平均に差はあるが、有意水準1%では差はない。
・有意水準1%で棄却域に入る
→2つののデータの平均に差はある。
(有意水準1%で棄却域に入るならば、有意水準5%でも棄却域に入るため、1%だけでよい)
9-2. 分散分析
分散分析とは、2つ以上のデータの平均に差があるかないかを調べる方法である。
対象となる複数のデータから『F』を計算する。そしてF分布での『F』の位置を調べることで、平均における差の有無が分かる。
『F』の計算方法
一度に計算すると大変なので、何段階かに分けて計算する。
まずは・・・
① 各データに対して、データの個数(=COUNT)、 平均(=AVERAGE)、標準偏差(=STDEVP)、分散(=VARP)を計算する。
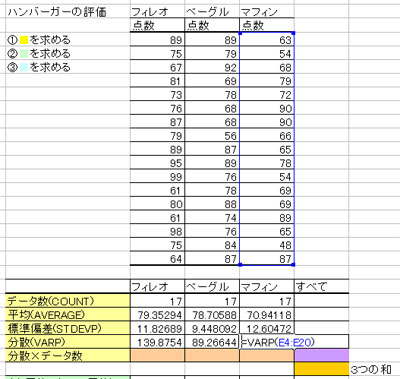
② データ全てに対して、データの個数(=COUNT)、 平均(=AVERAGE)、標準偏差(=STDEVP)、分散(=VARP)を計算する。
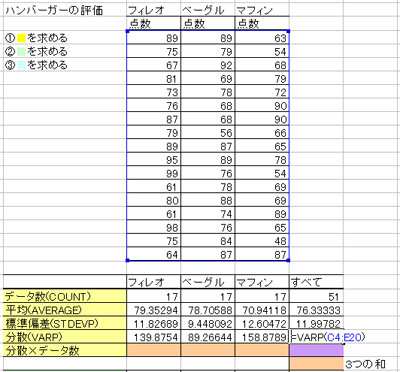
③ 各データと全てのデータにおいて、分散×データ個数を計算し、各データの分散×データ個数の合計を求める。
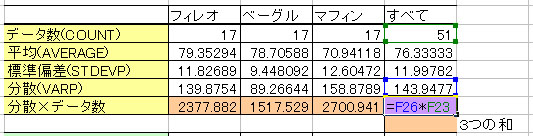
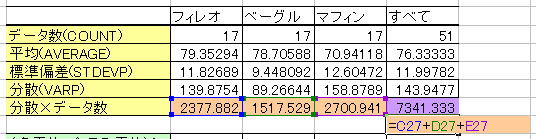
次に・・・
④ (各データの平均)-(全ての平均)を計算して2乗する。
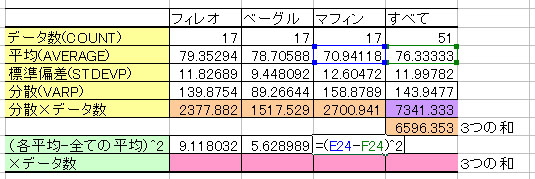
⑤ ④×データの個数 を計算する。
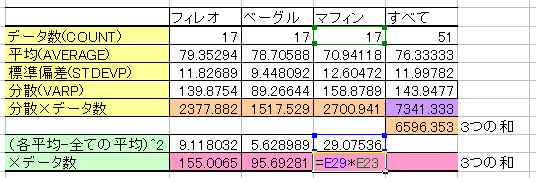
⑥ ⑤の各数値の合計を求める。
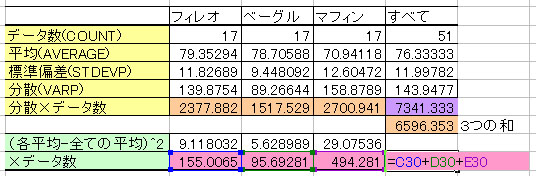
最後に・・・
⑦ 最後の表に数値を記入する。それぞれ同じ色のところにその数値を入れる。
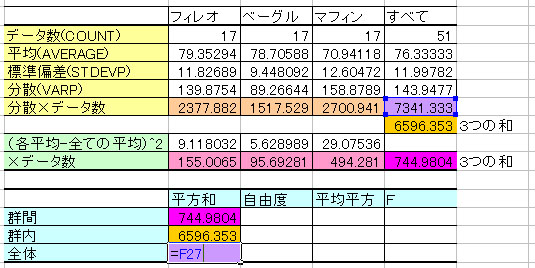
⑧ 自由度3種類を入力する。
1つ目は(データの種類-1)、2つ目は(データの総数-データの種類)、3つ目は(データの総数-1)
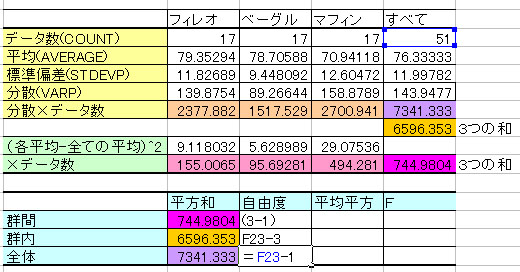
⑨ 1行目の数値において、⑦÷⑧を計算する。

⑩ 2行目の数値において、⑦÷⑧を計算する。

⑪ ⑨÷⑩を計算する。

⑫ Fが求まる。

実際は何もない状態からtを計算するのは難しい。そこで・・・
以前に分散分析を行ったファイルなどを見ながら、新たな分散分析を行う!
F分布の見方
少し甘め(有意水準5%)で調べる場合と、厳しめ(有意水準1%)で調べる場合の2つが選べる。
計算して求めた『F』の値が、 F分布のグラフの○部分(棄却域)に来るかどうかで、複数データの平均に差があるかが分かる。
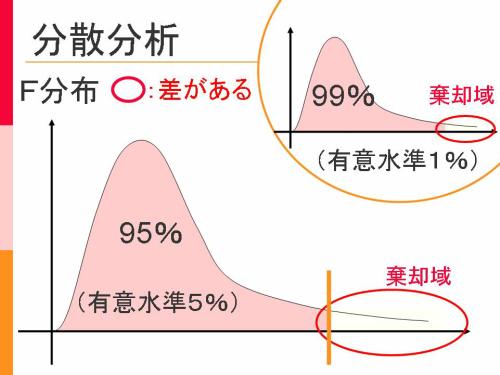
○部分(棄却域)の境界点は、t分布表から求まる。
Excelで『F』を求める際に、求めた『群内の自由度』と『群間の自由度』から境界点が分かる。
F分布表(有意水準5%) |
|||||
群内の自由度 |
群間の自由度 |
||||
1 |
2 |
3 |
4 |
5 |
|
10 |
4.96 |
4.10 |
3.71 |
3.48 |
3.33 |
20 |
4.35 |
3.49 |
3.10 |
2.87 |
2.71 |
30 |
4.17 |
3.32 |
2.92 |
2.69 |
2.53 |
40 |
4.08 |
3.23 |
2.84 |
2.61 |
2.45 |
50 |
4.03 |
3.18 |
2.79 |
2.56 |
2.40 |
60 |
4.00 |
3.15 |
2.76 |
2.53 |
2.37 |
70 |
3.98 |
3.13 |
2.74 |
2.50 |
2.35 |
80 |
3.96 |
3.11 |
2.72 |
2.49 |
2.33 |
90 |
3.95 |
3.10 |
2.71 |
2.47 |
2.32 |
100 |
3.94 |
3.09 |
2.70 |
2.46 |
2.31 |
200 |
3.89 |
3.04 |
2.65 |
2.42 |
2.26 |
300 |
3.87 |
3.03 |
2.63 |
2.40 |
2.24 |
F分布表(有意水準1%) |
|||||
群内の自由度 |
群間の自由度 |
||||
1 |
2 |
3 |
4 |
5 |
|
|
10 |
10.04 |
7.56 |
6.55 |
5.99 |
5.64 |
|
20 |
8.10 |
5.85 |
4.94 |
4.43 |
4.10 |
|
30 |
7.56 |
5.39 |
4.51 |
4.02 |
3.70 |
|
40 |
7.31 |
5.18 |
4.31 |
3.83 |
3.51 |
|
50 |
7.17 |
5.06 |
4.20 |
3.72 |
3.41 |
|
60 |
7.08 |
4.98 |
4.13 |
3.65 |
3.34 |
|
70 |
7.01 |
4.92 |
4.07 |
3.60 |
3.29 |
|
80 |
6.96 |
4.88 |
4.04 |
3.56 |
3.26 |
|
90 |
6.93 |
4.85 |
4.01 |
3.53 |
3.23 |
|
100 |
6.90 |
4.82 |
3.98 |
3.51 |
3.21 |
|
200 |
6.76 |
4.71 |
3.88 |
3.41 |
3.11 |
|
300 |
6.72 |
4.68 |
3.85 |
3.38 |
3.08 |
結論は3パターン
・有意水準5%で棄却域に入らない
→複数のデータの平均に差はない。
(有意水準5%で棄却域に入らないならば、有意水準1%でも棄却域に入らないため、5%だけでよい)
・有意水準5%で棄却域に入るが、有意水準1%で棄却域に入らない
→有意水準5%では複数データの平均に差はあるが、有意水準1%では差はない。
・有意水準1%で棄却域に入る
→複数のデータの平均に差はある。
(有意水準1%で棄却域に入るならば、有意水準5%でも棄却域に入るため、1%だけでよい)
今日はここまで
t検定における『t』の求め方や、t分布を使って結論の出し方、
分散分析における『F』の求め方や、F分布を使って結論の出し方をしっかり覚えよう。